模型

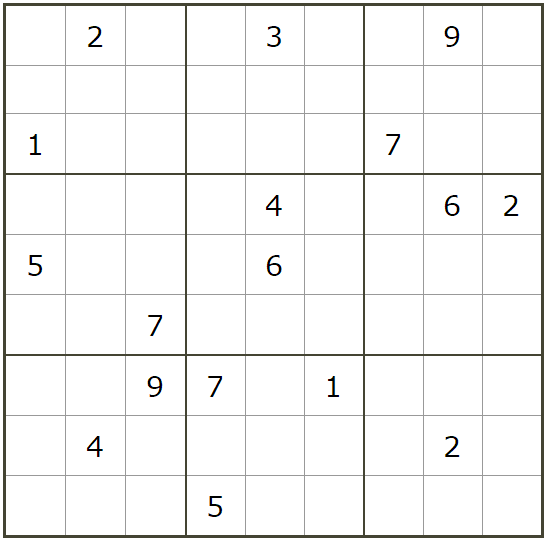
我们要给 数独游戏 建一个数学模型。通过求解这个模型，就可以得到数独游戏的解。

下标 link

为了方便描述，我们定义一些下标。

首先看 Block。用 i 和 j 代表一个 Block 所在的行和列，那么 Block(i,j) 就是第 i 行 j 列所在的块。因此 i 和 j 的取值范围是 1,2,3。

再看 Block 的内部。一个 Block 有 9 个格子。用 p 和 q 代表格子所在的行和列。因此 p 和 q 的取值范围也是 1,2,3。

这样一来，我们可以用下标 i,j,p,q 来定位一个格子。

再用 n 代表数字 1-9。

参数 link

用 a[i][j][p][q][n] 代表格子中是否填入数字 n。它的取值范围是 0, 1，其中 0 代表否，1 代表是。

• Block(1,1)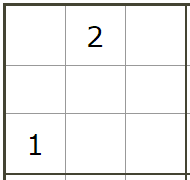

  

  a[1][1][1][2][2]=1

  a[1][1][3][1][1]=1

• Block(1,2)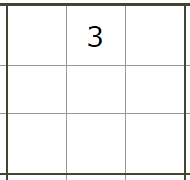

  

  a[1][2][1][3][3]=1

• Block(1,3)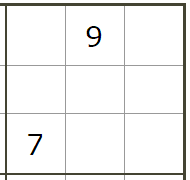

  

  a[1][3][1][2][9]=1

  a[1][3][3][1][7]=1

• 依此类推。其余的值都是 0。

变量 link

变量就是在空格子中需要填入的数字。

用 x[i][j][p][q][n] 来表示。它代表在 Block(i,j) 中第 p 行 q 列是否填入数字 n。它的取值范围是 0,1，其中 0 代表否，1 代表是。

约束 link

根据数独的规则，我们用数学语言进行描述。

1. 已经存在的值不能修改。 $$ x_{i,j,p,q, n} \geq a_{i,j,p,q,n},\quad \forall i,j,p,q, n $$

2. 一个单元格同时只允许填入一个数字。 $$ \sum_n x_{i,j,p,q,n} = 1, \quad \forall i,j,p,q $$

3. 每个块包含数字 1-9。 $$ \sum_{p, q} x_{i,j, p, q, n} = 1,\quad \forall i, j, n $$

4. 每行包含数字 1-9。 $$ \sum_{j, q} x_{i,j,p,q,n} = 1, \quad \forall i,p, n $$

5. 每列包含数字 1-9。 $$ \sum_{i, p} x_{i,j,p,q,n} = 1, \quad \forall j,q, n $$

目标 link

数独没有优化目标，只要求出满足约束条件的可行解即可。为了形式上的规范，目标函数可以写成一个任意的常数。

模型 link

综上所述，我们得到下面的整数规划问题。

求解这个模型，可以得到 $x$ 的值。