求解

有了数独模型，接下来是求解。实现一个类 SudokuModel，用来解数独对应的整数规划问题。

  
class SudokuModel(object):

    def __init__(self, a):
        """
        :param a: a[i][j][p][q][n] = 1 
                  if n is in cell [i][j][p][q] else 0
        """
        self.x = None  # solution 
    
    def solve(self):
        """ Solve the model.
        """
        pass

其中 solve 方法进行求解，结果保存在成员变量 self.x 中。可以用 OR-Tools 来实现求解。细节这里不多讲，请直接看代码。

说明一下输出参数。看这个例子。

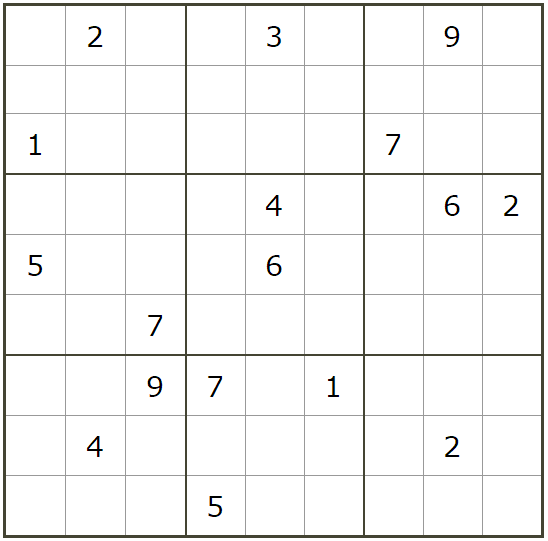
它对应的输入参数 a 如下。注意下标是从 0 开始。数字 1-9 对应下标 0-8。

  import numpy as np


a = np.zeros((3, 3, 3, 3, 9))

# Block[0][0]
a[0][0][0][1][1] = 1  # Number: 2
a[0][0][2][0][0] = 1  # Number: 1
# Block[0][1]
a[0][1][0][1][2] = 1  # Number: 3
# Block[0][2]
a[0][2][0][1][8] = 1  # Number: 9
a[0][2][2][0][6] = 1  # Number: 7
# Block[1][0]
a[1][0][1][0][4] = 1  # Number: 5
a[1][0][2][2][6] = 1  # Number: 7
# Block[1][1]
a[1][1][0][1][3] = 1  # Number: 4
a[1][1][1][1][5] = 1  # Number: 6
# Block[1][2]
a[1][2][0][1][5] = 1  # Number: 6
a[1][2][0][2][1] = 1  # Number: 2
# Block[2][0]
a[2][0][0][2][8] = 1  # Number: 9
a[2][0][1][1][3] = 1  # Number: 4
# Block[2][1]
a[2][1][0][0][6] = 1  # Number: 7
a[2][1][0][2][0] = 1  # Number: 1
a[2][1][2][0][4] = 1  # Number: 5
# Block[2][2]
a[2][2][1][1][1] = 1  # Number: 2

然后求解这个例子。

  if __name__ == '__main__':
    sm = SudokuModel(a)
    sm.solve()
    print(f"Solution:\n {sm.x}")

得到下面的结果。

  [[
    # Block(1, 1)
    [
        # Row 1, Col 1: Number 7
        [[0 0 0 0 0 0 1 0 0]
        # Row 1, Col 2: Number 2
        [0 1 0 0 0 0 0 0 0]  
        # Row 1, Col3: Number 4
        [0 0 0 1 0 0 0 0 0]] 
    
        # Row 2, Col 1: Number 3
        [[0 0 1 0 0 0 0 0 0]
         # Row 2, Col 2: Number 5
        [0 0 0 0 1 0 0 0 0]
         # Row 2, Col 3: Number 6
        [0 0 0 0 0 1 0 0 0]]
        
        # Row 3, Col 1: Number 1
        [[1 0 0 0 0 0 0 0 0]
        # Row 3, Col 2: Number 9
        [0 0 0 0 0 0 0 0 1]
        # Row 3, Col 3: Number 8
        [0 0 0 0 0 0 0 1 0]]
    ]
    
    # Block(1, 2)
    [
        [[1 0 0 0 0 0 0 0 0]
        [0 0 1 0 0 0 0 0 0]
        [0 0 0 0 0 0 0 1 0]]

        [[0 0 0 1 0 0 0 0 0]
        [0 0 0 0 0 0 1 0 0]
        [0 0 0 0 0 0 0 0 1]]

        [[0 0 0 0 0 1 0 0 0]
        [0 0 0 0 1 0 0 0 0]
        [0 1 0 0 0 0 0 0 0]]
    ]

    # Block(1, 3)
    # ...
    # Block(2, 1)
    # ...
    # Block(2, 2)
    # ...
    # Block(2, 3)
    # ...
    # Block(3, 1)
    # ...
    # Block(3, 2)
    # ...
    # Block(3, 3)
    # ...

]]

最后，我们得到下面的解。

  [[7 2 4 1 3 8 6 9 5]
 [3 5 6 4 7 9 2 1 8]
 [1 9 8 6 5 2 7 4 3]
 [9 1 3 8 4 7 5 6 2]
 [5 8 2 9 6 3 4 7 1]
 [4 6 7 2 1 5 3 8 9]
 [6 3 9 7 2 1 8 5 4]
 [8 4 5 3 9 6 1 2 7]
 [2 7 1 5 8 4 9 3 6]]

现在我们已经能够用 SuduokuModel 求解数独问题。但是这个过程太麻烦了。首先需要把结果转化成模型要求的输入，最后再把模型的结果转换成对应的数字。手动转换还容易出错。更好的做法是让程序自动转换输入和输出的格式。

Edit this page

Last updated 04 Jul 2025, 08:25 +0800 . history

模型

代码