On this page
article
如何写对偶问题
讲一下怎么手写线性规划的对偶问题。
形式
先记住对偶的基本形式。然后按照这个形式去写它的对偶问题。
从最小化问题开始。注意不等式符号是小于等于。
$$
\begin{aligned}
\min~ & c^Tx \\
\text{s.t. } & Ax \geq b \\
& x\geq 0
\end{aligned}
$$
其中 $A \in \mathbb{R}^{m\times n}, b\in \mathbb{R}^m, c, x\in \mathbb{R}^n$。
它的对偶问题定义如下。
$$
\begin{aligned}
\max~ & b^Ty \\
\text{s.t. } & A^Ty \leq c\\
& y \geq 0
\end{aligned}
$$
注意:对偶问题的决策变量 $y$ 的维度是 $m$,即 $y\in \mathbb{R}^m$。
观察一下这两个问题形式上的区别。
- 优化方向: $\min ~ \leftrightarrow~\max$
- 约束方向: $\geq~\leftrightarrow ~\leq$
- 参数位置:$b$ 和 $c$ 位置互换
如果原问题的约束是等式形式。
$$
\begin{aligned}
\min~ & c^Tx \\
\text{s.t. } & Ax = b \\
& x\geq 0
\end{aligned}
$$
它的对偶就是这样。
$$
\begin{aligned}
\max~ & b^Ty \\
\text{s.t. } & A^Ty \leq c\\
\end{aligned}
$$
这种情况下,对偶变量 $y$ 没有非负要求。
步骤
前面介绍了线性规划的标准型(两种形式),以及相应的对偶问题。下面讲手写对偶问题的思路。
第一步,定义对偶变量
基本原则是,原问题一个约束对应对偶问题的一个变量。换句话说,对偶变量的维度等于系数矩阵的维度。
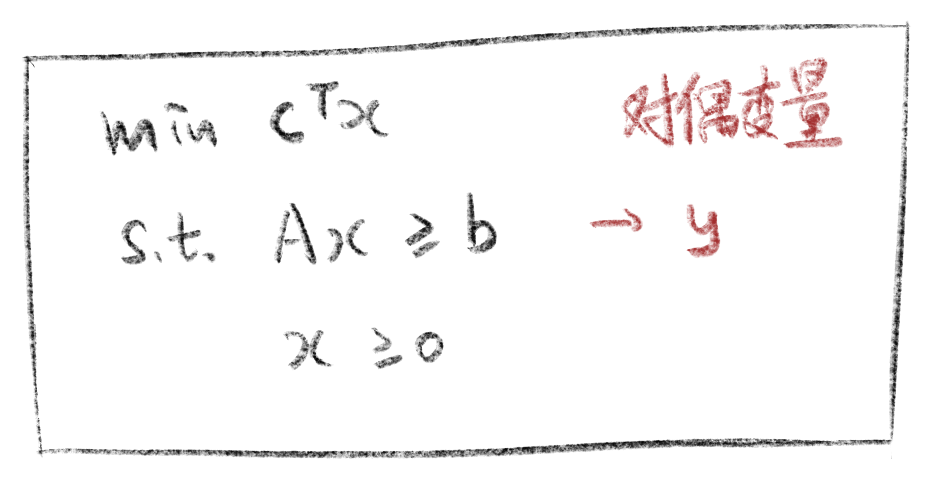
第二步,约束乘以变量
先得到目标函数,也就是不等式最右边部分。此外,如果原问题是最小化问题,那么对偶问题就是最大化问题。反之亦然。
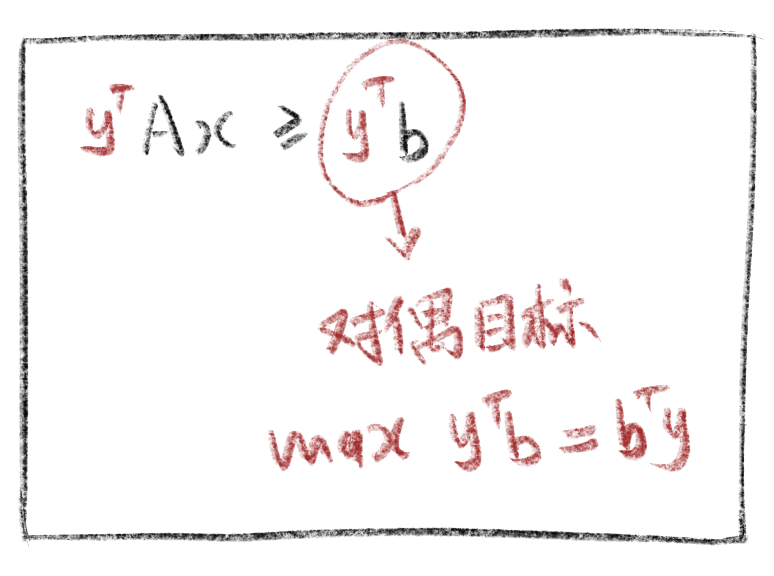
第三步,系数比较
然后得到约束条件。拿 $y^TA x$ 跟目标函数中 $c^Tx$ 中关于变量 $x$ 的系数进行比较。
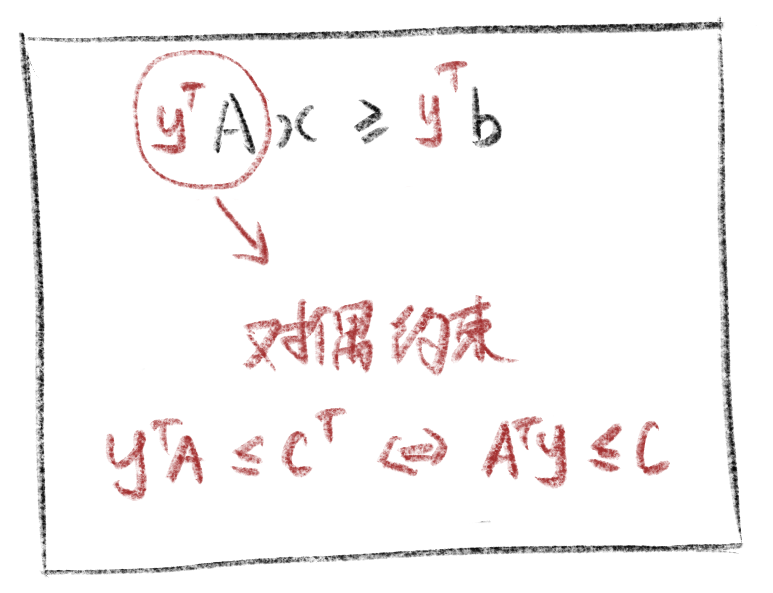
第四步,得到结果
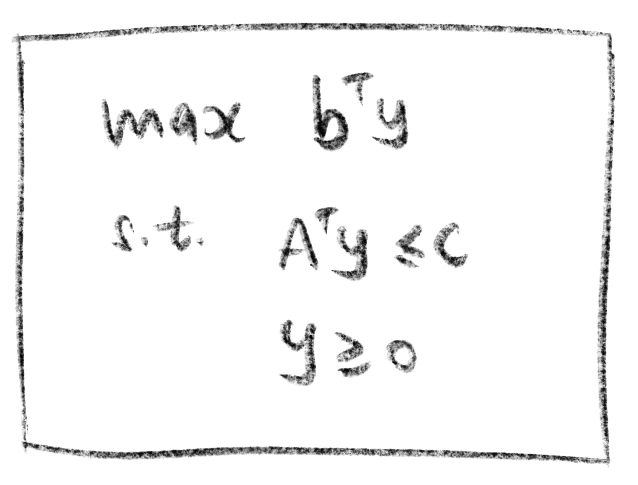
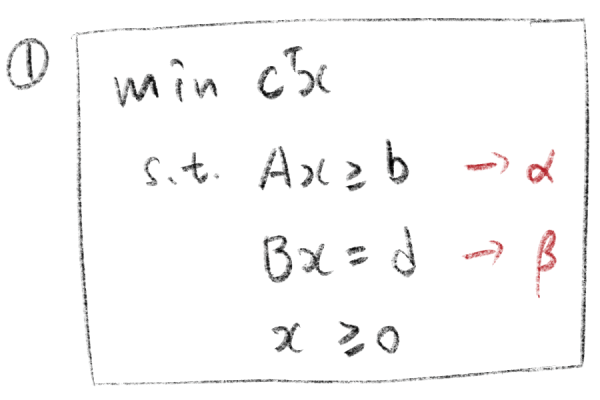
例 1
$$
\begin{aligned}
\min ~ & c^Tx \\
\text{s.t. } & Ax \geq b \\
& Bx = d \\
& x \geq 0
\end{aligned}
$$
下面是写对偶的过程。
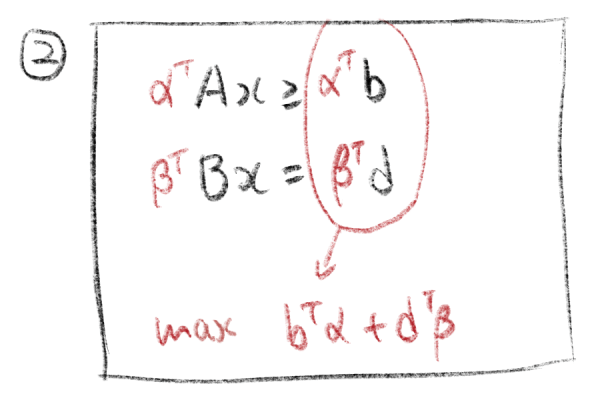
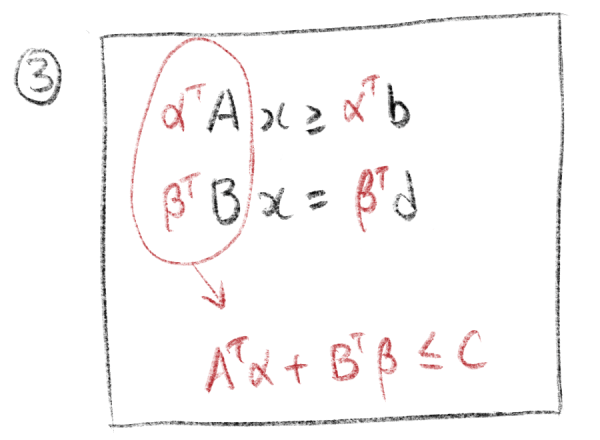
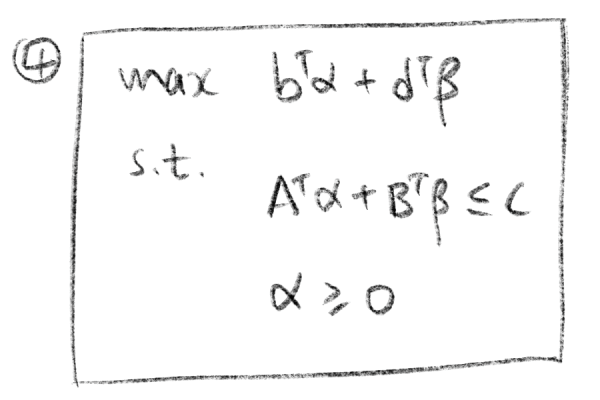
例 2
$$
\begin{aligned}
\min~ & -50x_1 + 20x_2\\
\text{s.t. } & 2x_1-x_2 \geq -5\\
& 3x_1+x_2\geq 3 \\
& 2x_1 -3x_2 \leq 12 \\
& x_1,x_2 \geq 0
\end{aligned}
$$
注意第三个不等式,它的方向是小于等于。可以先写成大于等于,然后再写它的对偶。
下面是写对偶的过程。


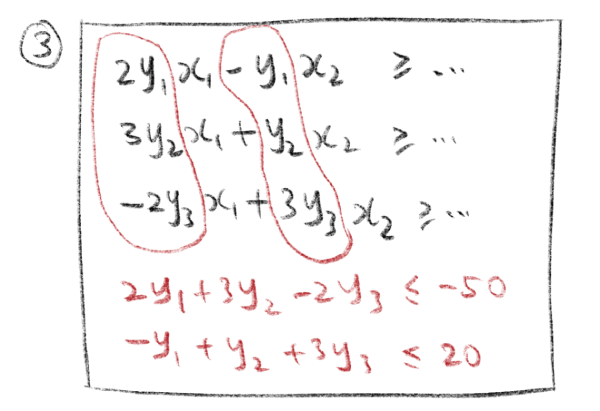

Last updated 03 Nov 2025, 09:34 +0800 .